Every now and then, a somewhat ambiguous mathematical expression starts trending on social media, and a bunch of people who haven't done any math since high school start arguing about the order of operations. Here's the latest contentious equation:
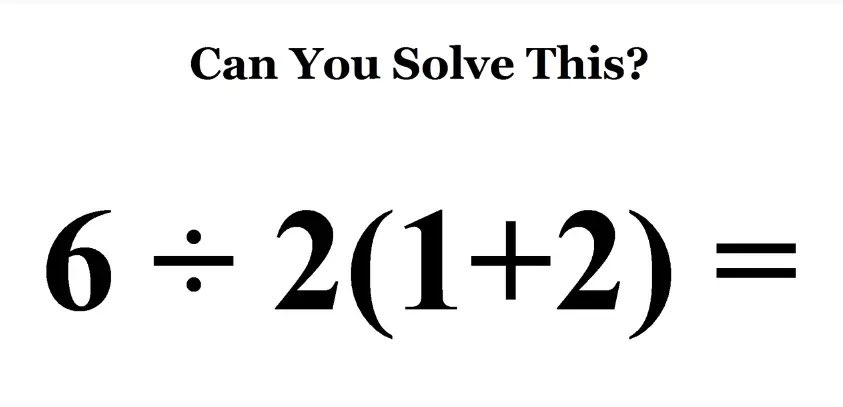
If you follow the standard BEDMAS/PEMDAS order of operations taught in school, and evaluate equal-precedence operations (i.e. division and multiplication) in order from left to right, then the expression is clearly equal to 9.
However, if you treat the implicit multiplication by juxtaposition as taking precedence over explicit division, you instead get 1. The latter convention is not usually taught in schools, but it's arguably more reflective of how the notation is used in practice; many mathematicians/scientists/programmers will deny ever having heard of this, but will readily admit that they read 1 / 2x as 1/(2x) and not x/2.
Like language, mathematical notation does not have an inherent, god-given meaning. Its only "meaning" comes from usage. And in practice, the '÷' symbol is basically never used by "real" mathematicians, who generally prefer a fraction bar. On the rare occasions when mathematicians do use an infix operator for division (i.e. '/') they tend to add parentheses to avoid any notational ambiguity (or they're using a calculator or programming language, in which case there won't be any multiplication by juxtaposition). So the expression presented above is arguably not even a well-formed expression according to the conventions actually followed (if not taught) by mathematicians.
This argument gets rehashed every time one of these equations goes viral, and I don't really want to get sucked in to that well-trodden debate, but it's an excellent justification for mentioning the following:
Dijkstra's Thoughts on Math Notation
I decided to write this blog post mainly to talk about The Notational Conventions I Adopted, and Why1 by famed computer scientist E. W. Dijkstra. It's an interesting read2, and a great reminder that mathematical notation is not set in stone, and that we can (and should) consider the utility and clarity of our mathematical notation. But more to the point of this blog post, the section on rules of priority is particularly relevant to the internet's perennial "BEDMAS debate."
Dijkstra says that he has "come to appreciate the following customs"3:
- Only use priority rules that are frequently appealed to, and hence are familiar. I would not hesitate to write p+q·r, but would avoid p/q·r and p ⇒ q ⇒ r.
- When you have the freedom, choose the larger symbol for the operator with the lower binding power.
-
Surround the operators with the lower binding power with more space than those with a higher binding power. E.g.,
p∧q ⇒ r ≡ p ⇒ (q⇒r)
is safely readable without knowing that ∧ ⇒ ≡ is the order of decreasing binding power. This spacing is a vital visual aid to parsing and the fact that nowadays it is violated in many publications means that these publications do a disservice to the propagation of formal techniques. (The visual aid is vital because the mathematician does not do string manipulation but manipulation of parsed formulae: when substituting equals for equals, identifying subexpressions is essential.)
How is this relevant?
First of all, note that in point 1 the order of division and multiplication is explicitly given as an example of unclear notation, despite there being an established order of operations (i.e. BEDMAS), since in practice this rule is not "frequently appealed to" and therefore not "familiar" (even though Dijkstra would obviously have been taught the BEDMAS order of operations or something equivalent).
Second, note that if the viral expression is intended to evaluate to 9, then it violates points 2 and 3; the use of no symbol whatsoever, which is arguably the smallest possible symbol, suggests that multiplication should be performed before the division, and there is substantial spacing around the ÷ symbol which again visually implies that it should be given lower precedence, since 2(1+2) appears as a single contiguous subexpression.
Given all this, it's no wonder that some people naturally read the expression "wrong."
On the subject of implicit multiplication in particular, check out this later section:
A.N. Whitehead made many wise remarks it is a pleasure to agree with, but I cannot share his judgement when he applauds the introduction of the invisible multiplication sign. The multiplication being so common, he praises the mathematical community for the efficiency of its convention, but he ignores the price.
[One] price is confusion: look at the different semantics of juxtapositions in:
3½ 3y 32
Is it a wonder that little children (many of whom have a most systematic mind) get confused by the mathematics they are taught? One would like the little kids to spend their time on learning the techniques of effective thought, but regrettably they spend a lot of it on familiarizing themselves with odd, irregular notational conventions whose wide adoption is their only virtue.
In addition to the fact that implicit multiplication does indeed cause confusion in the context of the viral expression, it's hard not to see the whole BEDMAS/PEMDAS debate as further proof that students "regrettably spend a lot of time on familiarizing themselves with odd, irregular notational conventions whose wide adoption is their only virtue."4
For related complaints about math education, be sure to check out A Mathematician's Lament by Paul Lockhart. If you're pressed for time, at least give the first two pages a chance.
A Deeper Philosophical Divide
In his introduction, Dijkstra discusses a philosophical division among mathematicians that affects attitudes towards notation:
As a final influence I must mention our desire to let the symbols do the work —more precisely: as much of the work as profitably possible—. The intuitive mathematician feels that he understands what he is talking about and uses formulae primarily to summarize situations and relations in to him familiar universes. When he seems to derive one formula from another, the transformations he allows are those that seem to be true in the universe he has in mind. The formalist, however, prefers to manipulate his formulae, temporarily ignoring all interpretations they might admit, the rules for the permissible symbol manipulations being formulated in terms of those symbols: the formalist calculates with uninterpreted formulae. While the average intuitive mathematician is perfectly happy with semantically ambiguous formulae “because he knows what is meant”, the formalist obviously insists on an unambiguous formalism.
Saying that the preferences of the formalist are not universally shared, would be the understatement of the year: intuitive mathematicians can hate more formally inclined colleagues with the same visceral hatred as Republicans can hate Democratic presidents with.
Whenever the "BEDMAS debate" starts up, it's hard not to find some commentators who are very angry at the implication that a mathematical expression could be at all ambiguous; this is despite demonstrable disagreement regarding the correct interpretation of the expression. I wonder to what extent this rejection of ambiguity is rooted in people's unexamined philosophical ideas about mathematics.
- I've linked to an HTML version, which includes a link to the original handwritten text that better displays the notations being described. ↩
- If you're into this sort of thing, anyways... ↩
- The wording and examples are verbatim from the original essay, but the numbering is my own. ↩
- See also the "FOIL method," which a) is pointless if you understand the distributive property of multiplication, b) is useless as soon as you want to multiply anything other than binomials, and c) wrongly implies that there is a correct order to the terms in a product of binomials. ↩